Last Month's Solution - January 2026
Here's the maze given for last month's Mazelog competition, together with the solution and details of the correct entries.
Lost Arrows (easy)
This a type of Arrow Maze (see Arrow Mazes); Start on the arrow in the top left corner. From that arrow move to any one of the arrows it's pointing to, in the same row, column, or diagonal. Continue in this way, following successive arrows, and find the shortest route to the target in the bottom right corner.
However, there's a slight problem: the illustrator missed out three of the arrows. To solve the maze you'll first have to work out the missing arrows.
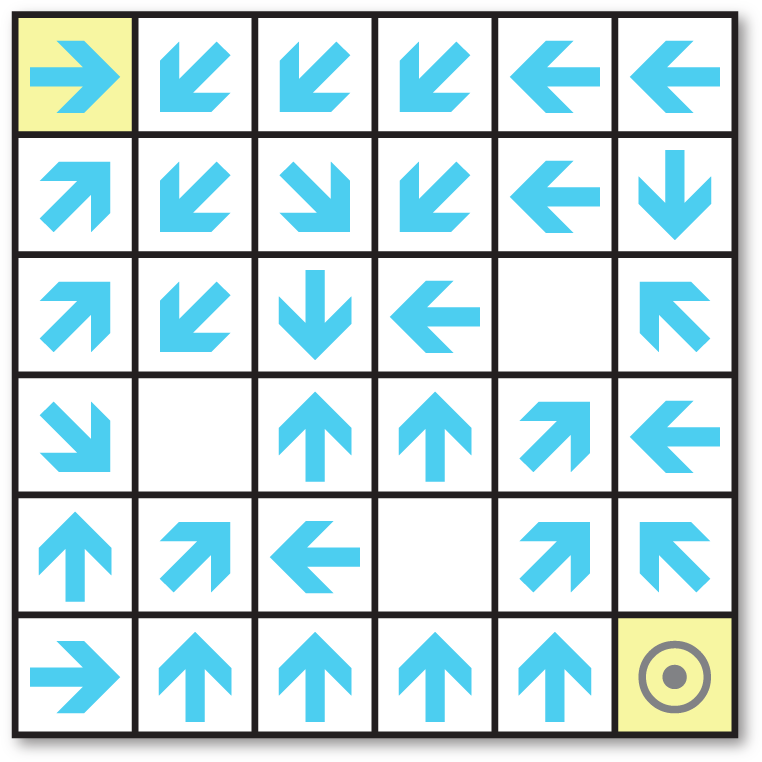
- Congratulations! Maze completed in %n steps and %s seconds.
Click to trace the route and solve the maze.
Lost Arrows Solution
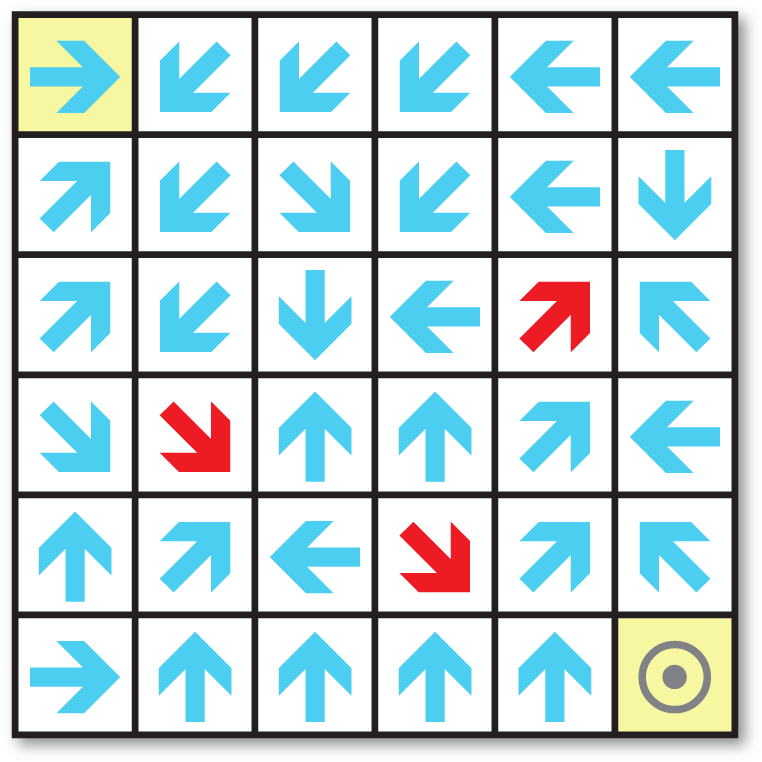
The key to finding the missing arrows is to work backwards from the goal. The only arrows that can reach the goal are the ones on squares 12 and 31, but the latter has nothing that can reach it. The only arrow that can reach the arrow on square 12 is the one on square 17, so that must be pointing NE.
Likewise, the only arrow that can reach square 17 is the one on square 35, and the only arrow that could reach that is the one on square 28, so that must be pointing SE.
Continuing to work backwards you can fill in the other missing arrow, and then solve the maze.
Here's the 12-step solution:
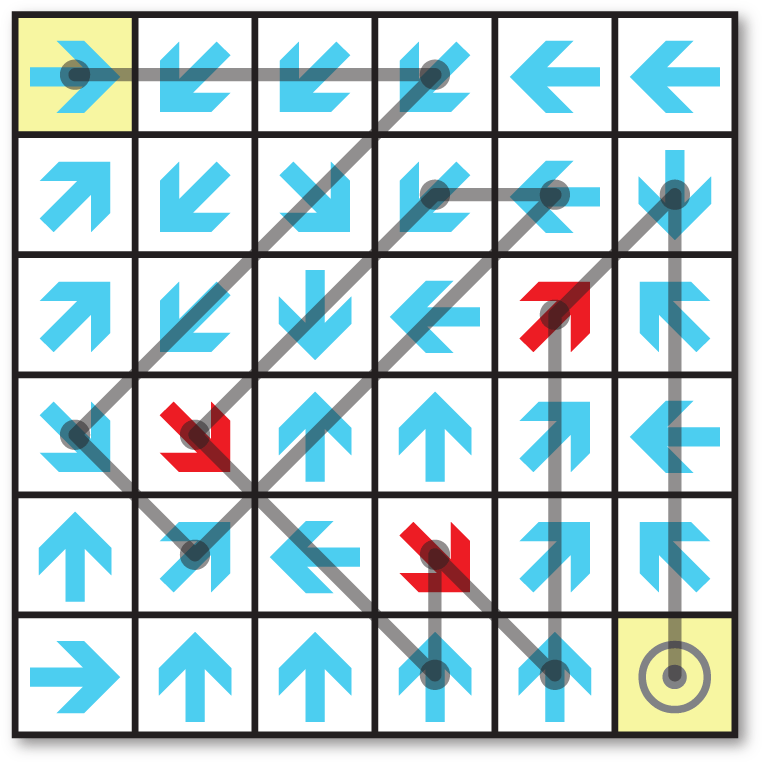
The sequence of cells is as follows:
1 4 19 26 11 10 20 34 28 35 17 12 36
Correct Entries
Correct entries were received from: nh_ngan26526, Mikhael Goikhman, and skeeto.
